15.2 应用实例

15.2.1 计算连续整数的和

循环解法

// 从 from 一直加到 to
// 循环解法:  
def sum1(from: BigInt, to: BigInt): BigInt = {
    var num = from
    var sum: BigInt = 0
    while (num <= to) {
        sum += num
        num += 1
    }
    sum
}

递归解法

// 递归解法
// f(m, n) = m + f(m + 1, n)
def sum2(from: BigInt, to: BigInt): BigInt = {
    if (from == to) from
    else from + sum2(from + 1, to)
}

说明:

• 递归算法，一般来说比较简单，符合人们的思维方式，但是由于需要保持调用堆栈，效率比较低，在调用次数较多时，更经常耗尽内存。

• 因此，程序员们经常用递归实现最初的版本，然后对它进行优化，改写为循环以提高性能。尾递归于是进入了人们的眼帘。

• 上面的这个递归调用不是尾递归, 因为有一次额外的加法调用, 这导致每一次递归调用留在堆栈中的数据都必须保留. 所以很容易出现StackOverflowError.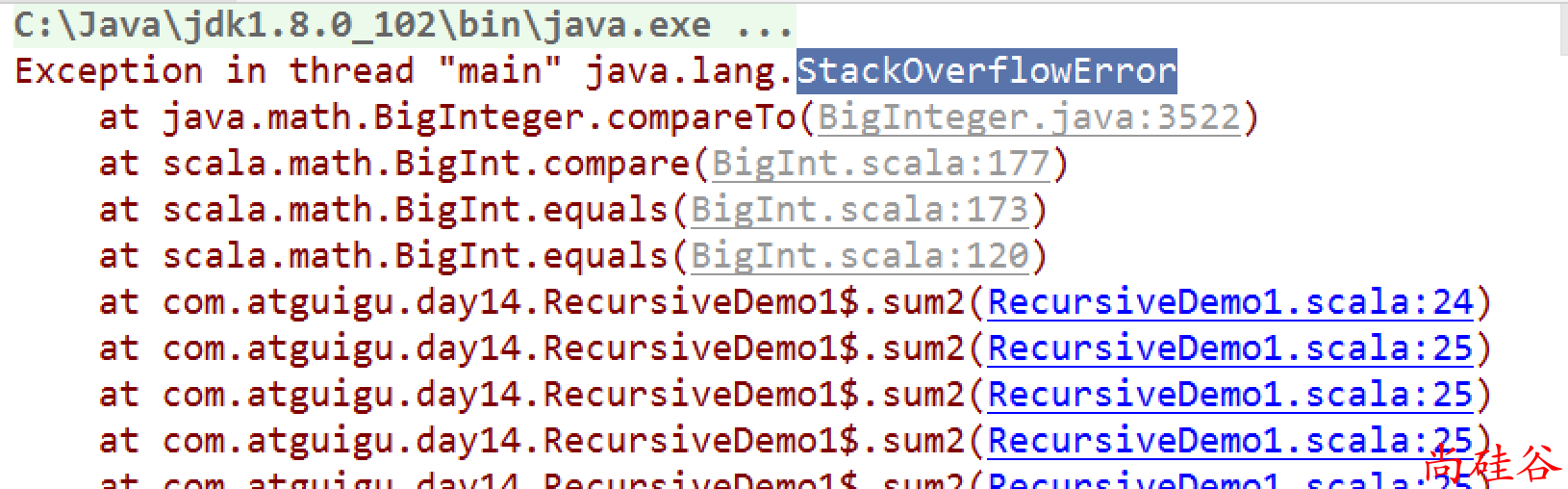

什么是尾递归

尾递归是指递归调用是函数的最后一个语句，而且其结果被直接返回，这是一类特殊的递归调用。

由于递归结果总是直接返回，尾递归比较方便转换为循环，因此编译器容易对它进行优化。现在很多编译器都对尾递归有优化，程序员们不必再手动将它们改写为循环。

上面的递归改成尾递归:

// 尾递归
def sum3(from: BigInt, to: BigInt, sum: BigInt): BigInt = {
    if (from == to) from + sum
    else sum3(from + 1, to, sum + from)
}

说明:

• 以上的调用，由于调用结果都是直接返回，所以之前的递归调用留在堆栈中的数据可以丢弃，只需要保留最后一次的数据，这就是尾递归容易优化的原因所在

• 而它的秘密武器就是上面的sum，它是一个累加器（accumulator，习惯上翻译为累加器，其实不一定非是“加”，任何形式的积聚都可以），用来积累之前调用的结果，这样之前调用的数据就可以被丢弃了。

• scala 已经对尾递归做了优化, 可以放心使用.(TCO: tail call optimization)

• 如果自己不确定是否为尾递归, 可以加注解:scala.annotation.tailrec. Scala 可以判断是否为尾递归,如果不是则会报错.

• 将一个常规递归改写成尾递归并不难。我们可以做预计算，将部分结果放置在参数中，而不是在递归调用方法返回的时候做乘法操作。

循环和递归执行效率的测试

package com.atguigu.day14
import scala.annotation.tailrec
object RecursiveDemo1 {
    def main(args: Array[String]): Unit = {
        val start1 = System.currentTimeMillis();
        System.out.println("循环开始时间: " + start1);
        println("循环计算结果 :" + sum1(1, 100000000))
        System.out.println("循环耗时: " + (System.currentTimeMillis() - start1));


        val start2 = System.currentTimeMillis();
        System.out.println("递归开始时间: " + start2);
        println("递归计算结果 :" + sum3(1, 100000000, 0))
        System.out.println("递归耗时: " + (System.currentTimeMillis() - start1));

    }

    // 循环解法
    def sum1(from: BigInt, to: BigInt): BigInt = {
        var num = from
        var sum: BigInt = 0
        while (num <= to) {
            sum += num
            num += 1
        }
        sum
    }


    // 尾递归
    @tailrec
    def sum3(from: BigInt, to: BigInt, sum: BigInt): BigInt = {
        if (from == to) from + sum
        else sum3(from + 1, to, sum + from)
    }
}

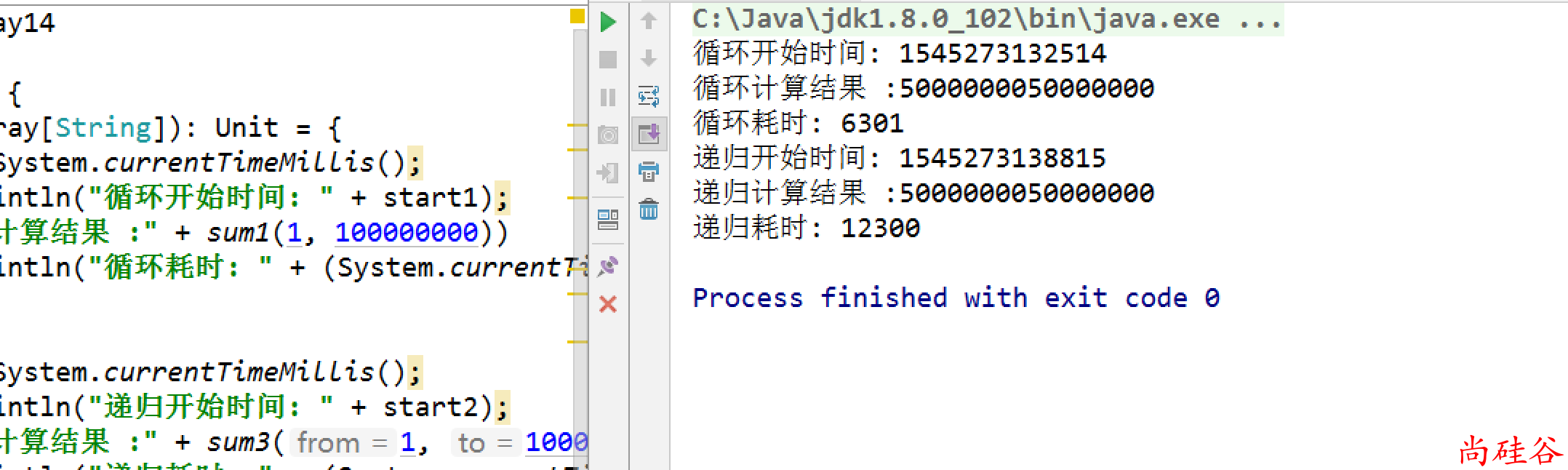
注意:

• 在数据量小的时候执行速度无差别.
• 在数据量大的时候, 递归执行效率会比循环差一些.

15.2.2 计算斐波那契数列第n项

非尾递归版本

def fibonacci(n: Int): Int = {
    if (n <= 2) 1
    // 不是直接返回函数调用, 而是有 + 运算, 所以不是尾递归
    else fibonacci(n - 1) + fibonacci(n - 2)  
}

尾递归版本

关键是找到前面所说的所谓"累加器".

/*
    n表示将来要计算第 n 项. 可以理解成需要计算 n 次
    acc2 就是我们要求的值
    假设计算第 5 项:
    第 1 次: f(5, 0, 1)  计算出来第 1 项
    第 2 次: f(4, 1, 1)  计算出来第 2 项
    第 3 次: f(3, 1, 2)  计算出来第 3 项
    第 4 次: f(2, 2, 3)  计算出来第 4 项
    第 5 次: f(1, 3, 5)  ...
 */
@tailrec
def fibonacci(n: Int, acc1: Int, acc2: Int): Int = {
    // 当 n==1 的时候表示是第 n 次计算, acc2就是我们需要的值了
    if (n == 1) acc2
    else fibonacci(n - 1, acc2, acc1 + acc2)
}

15.2.3 阶乘

@tailrec
def factorial(n: Int, acc: Long): Long = {
    if (n == 1) acc
    else factorial(n - 1, acc * n)
}

15.2.4 字符串翻转

@tailrec
def reverse(s: String, acc: String): String = {
    if (s.length == 0) acc
    else reverse(s.tail, s.head + acc)

}

15.2.5 计算最大值

@tailrec
def max(arr: Array[Int], m: Int): Int = {
    if (arr.length == 0) return m
    if (arr.head > m) max(arr.tail, arr.head) else max(arr.tail, m)
}

尾递归的局限

由于 JVM 的限制，对尾递归深层次的优化比较困难，因此，Scala 对尾递归的优化很有限，它只能优化形式上非常严格的尾递归。

1. 如果尾递归不是直接调用，而是通过函数值。 不能优化

2. 间接递归不会被优化 间接递归(有人叫做蹦床调用 trampoline call)，指不是直接调用自身，而是通过其他的函数最终调用自身的递归

总结:

• 使用递归可以对很多问题给出美观、直观以及富有表现力的解决方案。

• 然而，程序员往 往会避免递归或者不愿意使用递归，因为在输入值比较大的时候容易栈溢出。

• Scala 编译器内 置了递归优化，可以将尾部递归直接转化成迭代，从而避免栈溢出。这种优化让我们在能够使用递归简化代码时更加自由，无须担忧栈溢出。

• Java 没有对尾递归做优化, 所有在 Java 中使用不使用尾递归没有区别